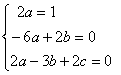|
Una equazione differenziale di ordine n
ha la forma:
 , oppure, esplicitando rispetto a yn, yn=f(x,y,y',.......yn-1)
. E' quindi una equazione nella quale compaiono la x, la
funzione y della stessa variabile e le sue derivate fino a quella dell'ordine ennesimo.Una funzione
y(x) è soluzione dell'equazione se la soddisfa,
cioè se
.
Le soluzioni prendono il nome di integrali .Questi ultimi
possono essere di due tipi integrale generale e integrale
singolare.
Quello generale è costituito da una famiglia di curve del tipo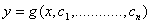 
, ciascuna delle quali, integrale particolare, si ottiene per arbitrari
valori reali delle costanti. L'integrale singolare invece non si ricava da quello generale.
Per meglio chiarire quanto affermato consideriamo il seguente esempio.
L'equazione differenziale del primo ordine
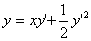
ha la famiglia di curve (in questo caso rette)
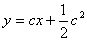 come integrale generale e la funzione
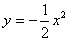 Ciò si può facilmente verificare determinando la derivata prima e sostituendo. Esistono vari tipi di equazioni differenziali.
Una prima classificazione può essere fatta in base
all'ordine.
Possono essere del primo, del secondo, del terzo
ordine ecc. Quelle che verranno esaminate e delle quali saranno
svolti degli esempi sono :
equazioni a variabili separabili;
equazioni lineari;
equazioni omogenee;
equazione di Clairaut;
equazione di Bernoulli.
Equazioni
a variabili separabili
Una equazione si dice a variabili separabili
se può essere ricondotta alla forma
y'=f(x)g(y) (1)
Per la soluzione si esprime
y' come
e si effettuano i calcoli
che seguono: moltiplicando ambo i membri per dx si ottiene:
  dividendoli per g(y) si ha:
 e integrando i due membri si perviene a:
 Quest'ultimo è l'integrale generale dell'equazione
(1).
Esempio.
    
+c Questa soluzione se si tiene conto delle proprietà
delle potenze si può scrivere
 cioè
(integrale generale)Equazioni lineari del primo ordine
Una equazione lineare del primo ordine è
del tipo 
(1)Per risolverla si considera l'equazione  Si determina poi l'integrale generale di quest'ultima che può essere scritto come  La costante si assume come funzione di x e la y si
considera come soluzione della (1) .
Cioè si sostituiscono nell'equazione (1) la funzione  e la sua derivata prima.
Questo metodo prende il nome di variazione della
costante arbitraria. Esempio Ci proponiamo di risolvere l'equazione  (1)
A tal fine consideriamo l'omogenea associata  il suo integrale generale, calcolato col metodo delle
variabili separabili, è    Ora consideriamo la costante come funzione di x e
calcoliamo la derivata  Sostituendo nella (1) otteniamo
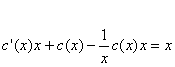 e semplificando
   c(x)=x+k
Sostituendo nella (2) si ricava l'integrale generale della (1) y=(x+k)x Al variare di k questa equazione rappresenta una famiglia di parabole. Si lascia come esercizio la verifica della soluzione. Equazioni lineari a coefficienti costanti Tralasciando quelle del I ordine risolvibili come
nel caso precedente, vogliamo esaminare l' equazione del II ordine
a coefficienti costanti 
(1) L'omogenea associata è 
.
( 2 )
Assumiamo la funzione  come soluzione. Sostituendo nella (2) la funzione
y e le sue derivate prima e seconda otteniamo: 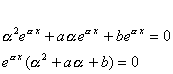  Quest'ultima prende il nome di equazione caratteristica
. L' omogenea associata ha integrale generale, a seconda che si abbiano due soluzioni reali e distinte, coincidenti o complesse coniugate, una delle seguenti funzioni rispettivamente: 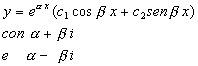   soluzioni dell'equazione caratteristica.
Si dimostra che se y è l'integrale generale
dell'omogenea associata e Y uno particolare della completa,
la soluzione generale della (1) si può scrivere come
y*=y+Y
L'integrale Y si determina in base alla funzione f(x). Con f(x)= 
,Y dovrà essere del tipo 
, se invece f(x) è un plinomio di grado m, Y
sarà un polinomio di grado s= n+m-k dove n rappresenta
l'ordine dell'equazione differenziale e k l'indice massimo dei coefficienti
diverso da zero. Gli indici si contano nell'equazione dal secondo
coefficiente di sinistra.Nel nostro caso a ha indice 1 e b 2. Esempio
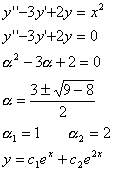 In questo caso s=2+2-2=2 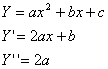 Sostituendo nell'equazione completa si ottiene: 2a-3(2ax+b)+2(a 
+bx+c)=
Eseguendo i calcoli si determina: 2a
+(-6a+2b)x+2a-3b+2c=
Per l' identità dei polinomi si può
srivere il sistema |
